
在上一篇笔记《变分量子对角化》里面我们简单介绍了一下VQSD的概念,接下来的这篇笔记才是最重要的部分,这篇文章我们的内容如下:
1. 原文代价函数是如何构造的?
2. 为什么说代价函数影响到了我们估计值的精确度?
3. 分析一下原文作者的实验,看一下迭代次数、估计值、角度、代价函数它们之间的关系。

默默告诉自己我一定得好好写写,冲鸭~
前面说到代价函数才是整个过程的核心,代价函数的构造涉及了很多的问题,因为我们要寻找一个最优的角度,角度的不断调整,会影响近似对角化的结果,代价函数是一个评判精度的参数,从下面这个式子中可以看出我们的目的就是要寻找一个使得代价函数最小的角度,这个角度我们称为αopt。
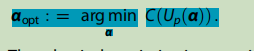
由上图我们可以看出cost function的取值肯定也是伴随着参数的调整而不断变化,当α取值为α1,代价函数达到最小值的时候,α1就是我们所要寻找的αopt之一,我们的目标就是寻找p个αopt,构造出一个最优的代价函数。
上面我们提到了局部最小值α1,意思就是α目前所处的区间,只有当α=α1的时候,代价函数的取值最小,那么我们就把α1称作局部最小值。但是如何衡量代价函数此时的取值是最小的呢,如果不是局部最小值我们接下来还要进行优化参数α,我们如果采用基于梯度的方式进行参数优化,就可以借助梯度来衡量此时的α1是不是我们所要寻找的局部最优值。
如果不太理解,就想一想导数和极值问题,思想是差不多的,梯度只是衡量当前α1是否为局部最小值的一个标准。
说到梯度,我们就要考虑噪声、梯度消失的问题,emem,反正我是不太懂的,还需要进修这个模块。只是先说一下本文的代价函数构造是如何解决巧妙地在梯度消失存在的情况下来训练U(θ),来进行参数α的优化。
首先说一下本文提及的short-depth电路,看看这个电路的面貌:
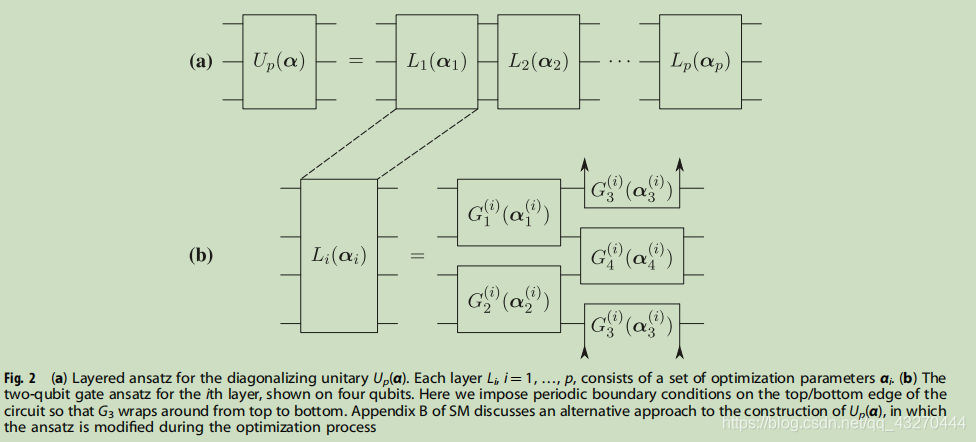
这个电路是如何缓解局部最小值的呢?将p层的优化参数作为p+1参数的起点,寻找下一个αopt.原文表达如下:

据我师兄所讲,其中的barren plateaus指的是平原和高峰,指的是梯度有高有低。对于代价函数C1而言,在局部最小值附近,它的梯度变化很剧烈(后面会给出解释),但是一旦远离了局部最小值,它的梯度又会消失。
(PS :关于barren plateaus 我得去看看原文,后期再整理一下相关的概念~)
写到这里我自个都搞晕了,代价函数C1仍旧存在梯度消失,梯度变化剧烈的情况,怎么敢信誓旦旦地说缓解了局部最小值问题。然后我就跑去问我贼厉害的师兄,发现果然是我理解的不够透彻。

原文作者在进行参数优化方面是一层一层的进行的,而不是所有的层数一起蹦迪,那样的话后期参数调整所需要的工程量太大了。所以他们提出先把眼前的利益放进口袋里,然后再打算慢慢地赚它一个亿。这样想来的话,局部最小值问题确实得到了优化。
如果还不理解的话,想想这句话“再小的问题乘以十三亿,那也会是个很大的问题”,那么本文的原则就是将大问题除以十三亿,转化成小问题,一步步的解决,那么这个过程中遇到的困难就没有那么可怕了。
再说一下原文给出的代价函数的要求:

faithful:代价函数为0,除非就是我们估计的和原来的信息一模一样,不然我们理想的代价函数就是无限趋近于0,但还是非0的一个参数;
efficiently computable:可以在多项式时间内完成;
operational meanings: 我们估计的特征值(特征向量)和实际的特征值(特征向量)之间的误差小于代价函数的取值;
在本文中代价函数构造为:

看懂没?肯定没看懂吧。。。。。

别着急我们慢慢来。为了更好地理解(7)、(8)我们先跳到另一个环节,话不多说,先上图:

在(7)式子中我们是针对全局标准基进行定义的,(7)式的后半部分代表的是去除非对角线元素所保留的密度矩阵Z(ρ),结合上图里面对于(20)、(21)、(22)的解释,***我们可以看出(7)式代表的意义就是ρ和ρ 之间对角线元素之间距离的平方和。(就如同我们计算的两点之间距离的平方)***
在(8)式中,我们是针对局部标准基进行定义的,(9)式说明只有我们近似得到的对角化矩阵和实际的对角化矩阵是相同的情况下,代价函数C1,C2才为0。
(你问我啥是全局标准基,啥是局部标准基,我这样回答你,全局标准基他们一家人,只要打扫卫生每个人都要去劳动;局部标注基他们一家打扫卫生,不要求一起劳动,单人行动模式,最后每个人的工作量取得是平均值)
由于C1,C2伴随着n的增加,效果各异。就像一条路肯定有高有低,坡度还不一样嘞,所以为了更好地训练U(θ),找到αopt,我们最后构造出的代价函数要充分考虑C1,C2受n的影响。原文解释如下:

q是一个自由参数,允许我们根据自己的实际问题来调整VQSD方法;对于小的n,q的取值近似为1;对于大的n,q的取值就可以设置的稍微小一点。下面给出了为什么不能用C1来训练U(θ)的详细解释:

通过将C1,C2相结合,即使n太大,C1的梯度消失,我们也可以通过C2来进行参数优化,进行局部最小值的寻找。
在这里我们好好捋一捋在这篇论文中会影响到我们近似对角化结果的参数有哪些。
| 符号 | 意义 |
|---|---|
| p | 超参数 |
| iterative numbers | 迭代次数:大,结果精确,,复杂度高 |
| fz | 读到特征值的次数:大,结果精确 |
| Nreadout | 读取次数:大,结果精确 |
| εmax | 特征值的相对误差,阈值 |
| vz~ | inferred eigenvector(eigenvalue):数值大,越精确 |
| αopt | 最优参数 |
| C | 代价函数:小,结果越精确 |
| λz~ | inferred eigenvalue:数值大,越精确 |
我们先来介绍一下特征值误差和特征向量误差的表示符号:
(1)特征值误差表示:

(2) 特征向量误差表示

内容总结:我们可以把式子(4)看作是一个加权特征向量误差,其中大特征值对应的特征向量权重相对而言比较大,那么我们想要减少误差,可以降低代价函数,从而迫使最大特征值对应的特征向量高度精确。
下面我们分析一下为什么我们会说代价函数C1是特征值误差的上界:


原文中是这样分析的:

推导过程如下:

由此看出,当代价函数C1越小,那么我们得到的特征值的误差就越小,同时特征向量的误差也就越小。

实验效果:
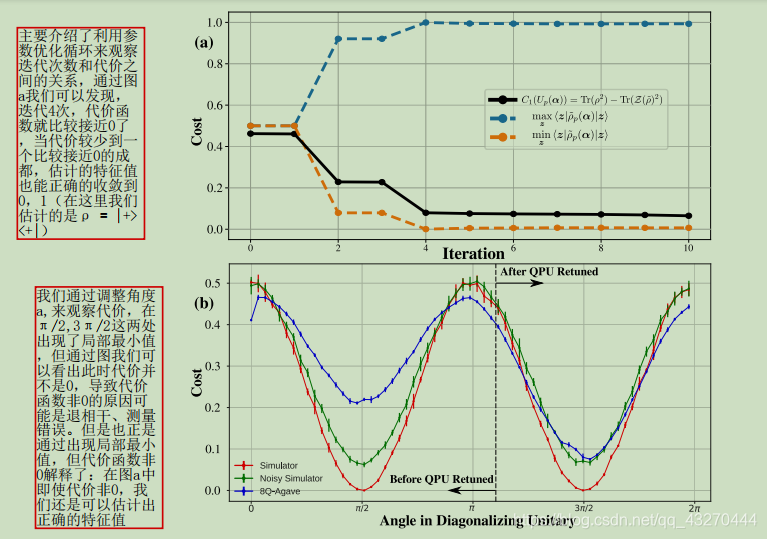
这里想要强调的是第二个图,在第二个图中我们发现在π/2,3π/2,代价函数出现了比较小的数值,并且在当时α所处的区间内,没有比这令代价函数还要小的数值,所以我们可以判断上面两个值就是局部最小值,是我们要寻找的αopt的一员,这里的图像比较具备周期性,结果比较形象直观,但并不是都可以找到局部最优值,就像在高等数学里面,我们的极小值可不一定是最小值。
1、EL表达式解析过程 JSP中,我们经常会写为${obj.name}字样,但你有没有想过,...
2015年Win10发布时,为刺激用户升级,微软祭出了免费大招,即允许Win7/8.1正版用...
栈是限定仅在表尾进行插入和删除操作的线性表 栈的结构定义如下 typedef struct ...
主要目的 a. 掌握获取 GridPanel 当前行的各个字段值的方法 b. 掌握如何将前台数...
在Python中实现正则的方式是通过re(regular expression的缩写)模块来实现的,...
Button用得挺多的,在这整理了下它的事件处理方法,发现实现方法还不少,我比较...
YUV4:2:0存储格式 分层存储按Y-U-V顺序是最常见的存储格式。如下图按颜色对应。 ...
js中的事件 什么是事件?事件是电脑输入设备与页面进行交互的响应,我们称之为事...
最近正是求职的高峰期目前也有很多求职的方式其中有许多内推的方式都是以邮件形...
本文将结合实例 demo,阐述 30 条有关于优化 SQL 的建议,多数是实际开发中总结...