【运筹学】对偶理论 : 对称理论示例 ( 对称理论 | 标准的原问题对偶问题 | 原问题目标函数求最小值示例 | 求对偶技巧 ) ★

韩曙亮

发布于 2023-03-28 20:34:22

7610

发布于 2023-03-28 20:34:22

文章被收录于专栏：韩曙亮的移动开发专栏韩曙亮的移动开发专栏

文章目录

一、对称理论

参考【运筹学】对偶理论 : 对称形式 ( 对称形式 | 对偶模型转化实例 | 对偶问题规律分析 ) 写出原问题线性规划的对偶问题线性规划 ,

原问题的线性规划模型 : 注意原问题的线性规划目标函数求最大值 , 约束方程都是小于等于不等式 ;

\begin{array}{lcl} \rm maxZ = C X \\\\ \rm s.t\begin{cases} \rm AX \leq b \\\\ \rm X \geq 0 \end{cases}\end{array}

如果原问题是求最大值 , 约束方程有大于等于不等式 , 需要在这些大于等于不等式左右两边乘以

\rm -1

, 将大于等于不等式转为小于等于不等式 ;

如果进行了上述操作 , 则最终求出对偶问题后 , 系数矩阵肯定不互为转置矩阵 , 还要进行一次代换 , 令

\rm y' = -y

吗使用

\rm -y' = y

替换对偶问题中的变量 ;

对偶问题的线性规划模型 : 对偶问题目标函数求最小值 , 约束方程都是大于等于不等式 ;

\begin{array}{lcl} \rm minW = b^T Y \\\\ \rm s.t\begin{cases} \rm A^TY \geq C^T \\\\ \rm Y \geq 0 \end{cases}\end{array}

矩阵转置 : 第

列变第

行 ,

\cdots

, 第

\rm n

列变第

\rm n

行 ;

二、对偶理论示例

对偶示例 : 给出如下线性规划 ,

\begin{array}{lcl} \rm maxZ = 2 x_1 + x_2 \\\\ \rm s.t\begin{cases} \rm x_1 - 2x_2 \leq 8 \\\\ \rm x_1, x_2 \geq 0 \end{cases}\end{array}

上述线性规划原问题 ① 目标函数求最大值 ② 约束方程是小于等于不等式 , ③ 约束变量大于等于

, 符合标准 ;

写出其对偶问题 :

( 1 ) 目标函数求最小 , 且目标函数的系数是原方程的约束方程常数 ;

\rm minZ = 8y_1

( 2 ) 约束条件 :

对偶问题约束方程系数 : 约束方程矩阵是

\begin{pmatrix} &1 & -2 & \\ \end{pmatrix}

的转置矩阵

\begin{pmatrix} &1 & \\ &-2 & \\ \end{pmatrix}

;

对偶问题变量个数 : 约束方程的变量个数是矩阵的列数 , 这里只有

列 , 则只有

个变量

\rm y_1

;

约束方程中间符号 : 约束条件的符号是由原问题变量符号决定 ( 都是

\geq 0

) , 因此对偶问题的约束方程符号也是

\geq

;

约束方程右侧常数 : 是原问题目标函数的系数转置 , 分别是

2 , 1

;

变量符号 : 对偶问题变量符号与原问题约束方程符号相反 ; 原问题约束方程是小于等于符号 , 对偶问题的变量是大于等于

的 ;

最终的对偶问题是 :

\begin{array}{lcl} \rm minW = 8y_1 \\\\ \rm s.t\begin{cases} \rm y_1 \geq 2 \\\\ \rm -2y_1 \geq 1 \\\\ \rm y_1 \geq 0 \end{cases}\end{array}

三、对偶理论示例 2

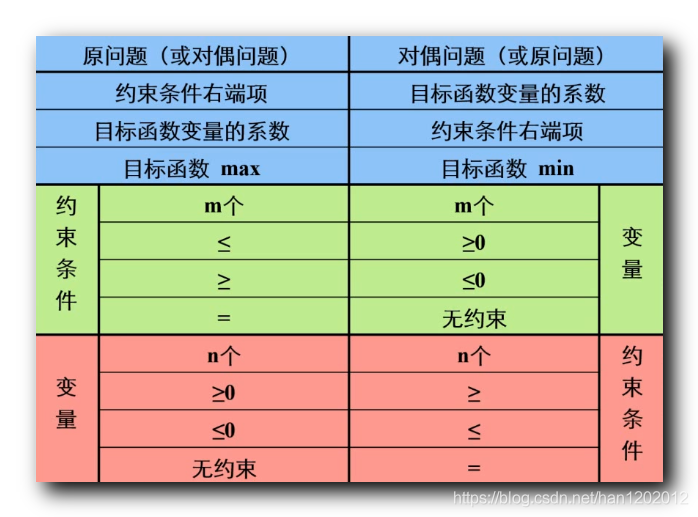
如果给出的原问题目标函数是求最小值 :

\begin{array}{lcl} \rm minZ = 2 x_1 + x_2 \\\\ \rm s.t\begin{cases} \rm x_1 - 2x_2 \leq 8 \\\\ \rm x_1, x_2 \geq 0 \end{cases}\end{array}

上述线性规划的对偶问题的目标函数是求最大值 ;

参考下图列表 :

写出其对偶问题 ( 上述表格中的右侧 ) :

( 1 ) 目标函数求最大 , 且目标函数的系数是原方程的约束方程常数 ;

\rm minW = 8y_1

( 2 ) 约束条件 :

对偶问题约束方程系数 : 约束方程矩阵是

\begin{pmatrix} &1 & -2 & \\ \end{pmatrix}

的转置矩阵

\begin{pmatrix} &1 & \\ &-2 & \\ \end{pmatrix}

;

对偶问题变量个数 : 约束方程的变量个数是矩阵的列数 , 这里只有

列 , 则只有

个变量

\rm y_1

;

约束方程中间符号 : 约束条件的符号是由原问题变量符号决定 ( 都是

\geq 0

) , 这里如果目标函数求最小值时原问题 , 其对偶问题约束方程符号与原问题变量符号相反 , 因此对偶问题的约束方程符号也是

\leq

;

约束方程右侧常数 : 是原问题目标函数的系数转置 , 分别是

2 , 1

;

变量符号 : 对偶问题变量符号与原问题约束方程符号相同 ; 原问题约束方程是小于等于符号 , 对偶问题的变量是小于等于

的 ;

最终的对偶问题是 :

\begin{array}{lcl} \rm maxZ = 8y_1 \\\\ \rm s.t\begin{cases} \rm y_1 \leq 2 \\\\ \rm -2y_1 \leq 1 \\\\ \rm y_1 \leq 0 \end{cases}\end{array}

四、求对偶技巧 ★★

写出对偶定理的标准对称形式 ★ : 记住下面的标准形式

原问题 :

\begin{array}{lcl} \rm maxZ = C X \\\\ \rm s.t\begin{cases} \rm AX \leq b \\\\ \rm X \geq 0 \end{cases}\end{array}

对偶问题 :

\begin{array}{lcl} \rm minW = b^T Y \\\\ \rm s.t\begin{cases} \rm A^TY \geq C^T \\\\ \rm Y \geq 0 \end{cases}\end{array}

查看约束变量的符号与其另外一个对偶问题的约束方程的符号一致性 , 来确定对偶问题的约束方程符号 ;

约束方程符号 :

如果当前线性规划问题目标函数是求最大值 , 原问题就是上面的问题 , 其对偶问题 ( 下面的 ) 的约束方程符号是

\geq

, 因此对偶问题的约束方程符号与原问题变量符号一致 ;

如果当前线性规划问题目标函数是求最小值 , 原问题就是下面的问题 , 其对偶问题 ( 上面的 ) 的约束方程符号是

\leq

, 因此对偶问题的约束方程符号与原问题变量符号相反 ;

变量符号 :

如果当前线性规划问题目标函数是求最大值 , 原问题就是上面的问题 , 其对偶问题 ( 下面的 ) 的约束方程符号是

\geq

, 因此对偶问题的变量符号与原问题约束方程符号符号相反 ;

如果当前线性规划问题目标函数是求最大值 , 原问题就是上面的问题 , 其对偶问题 ( 下面的 ) 的约束方程符号是

\geq

, 因此对偶问题的变量符号与原问题约束方程符号符号一致 ;

本文参与?腾讯云自媒体分享计划，分享自作者个人站点/博客。

原始发表：2020-12-31，如有侵权请联系 cloudcommunity@tencent.com 删除

变量

本文分享自作者个人站点/博客?前往查看

如有侵权，请联系 cloudcommunity@tencent.com 删除。

本文参与?腾讯云自媒体分享计划? ，欢迎热爱写作的你一起参与！

登录后参与评论

0 条评论

热度