关于奈奎斯特定理(Nyquist's Theorem)和香农定理(Shannon's Theorem)的理解
原创关于奈奎斯特定理(Nyquist's Theorem)和香农定理(Shannon's Theorem)的理解
原创先说说奈奎斯特采样定理:
我们需要对我们所收到的基带模拟信号(连续信号)进行采样;需要用到狄拉克梳妆函数(采样函数):
x(t) 是基带信号,频域形式为X(jw)= \left\{ \begin{array}{**lr**} X(jw), &|w|<w_m \\ 0, &|w|>w_m\ & \end{array} \right. ,
时域相乘进行采样,得到采样后的信号 s\left( t \right) \cdot x\left( t \right) \rightarrow \frac{1}{2\pi}S\left( jw \right) \otimes X\left( jw \right) =\frac{1}{2\pi T_s}\sum_{n=-\infty}^{\infty}{X\left( w-nw_s \right)}
即原X(jw)产生很多”分身“,拿往右平移的第一个"分身"为例,最小角频率为 w_{min}=w_s-w_m ,需保证w_{min}\ge w_m (即第二个分身的”头“应该大于前一个的”尾“)这样才不会产生重叠,即码间串扰。得出w_s\ge2w_m,f_s\ge2f_m, 采样得到的信号不会产生码间串扰,且可以推出T_s=\frac{1}{f_s}\le \frac{1}{2f_m} ,采样信号的周期也有相应的限制。
奈奎斯特定理:
这里Cmax指的是信道的最大容量(bps),B是信道的带宽,L还是信号电平的个数。
奈奎斯特定理适用的情况是无噪声信道,用来计算理论值。
这里的B(单位Hz),B=\frac{1}{T} ,T是码元持续时间(单位s), 所以B 的单位也可以表示成(symbol/s) ,就很容易理解(symbol/s)*(bit/symbol)=bit/s(bps) .
Q1: 为什么有B=\frac{1}{T} ?
假设有一时间长度为T的码元,其形状在时域为一门宽为T的门信号,不妨表示成 g_T\left( t \right) ,其频域形式:
由Sa函数的第一零点带宽可知,此码元信号的带宽(基带信号带宽)为:w_m=\frac{2\pi}{T},f_m=\frac{1}{T} ,这里的f_m=B (单位Hz).
Q2: 为什么取抽样率取2B,若波特率大于2B会发生码间串扰。
实际上数字信号是由一个个脉冲波形组成的,而信号在发送和接收时,都会经过低通滤波器,低通滤波器在频域为一门函数,关于纵坐标对称,现在假设这个滤波器性能非常理想,也就是具有门一样的方阵滤波效果,单个冲击加到滤波器上,输出的波形是这样的,
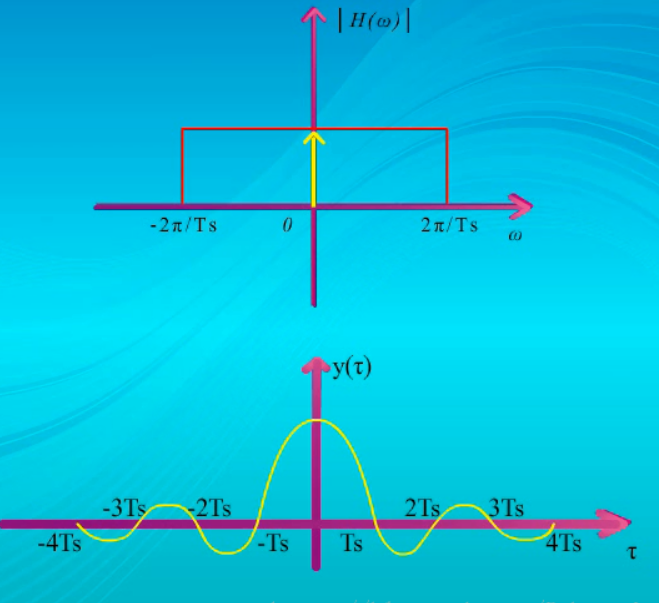
他妈的,他这个图有问题,此处y\left( t \right) =Sa\left( \frac{\pi}{T_s}t \right) \rightarrow T_sg_{\frac{2\pi}{T_s}}\left( w \right) ,频域的w_m=\frac{\pi}{T_s} ,它标的w_m=\frac{2\pi}{T_s} ,显然不对
这个输出波形的特点是具有很长的拖尾,幅度逐渐减弱,在时间轴上出现很多零点,
这些零点之间间隔均匀,都是Ts,
一个脉冲的冲击波形是这样的,那一串脉冲的输出波形是怎么样的呢?
应该是这样的:
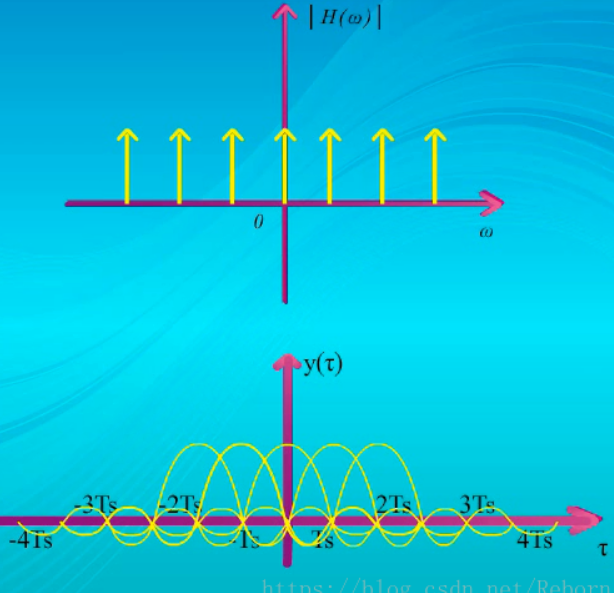
如果接收端的抽样判决时刻和脉冲序列是同步的,也就是正好都在Ts的整数倍处,进行判决,
那么在这些点上,就只有一个脉冲波形的振幅,其他脉冲波形的振幅在这些点上都为0,所以相互间没有码间串扰,能正确的恢复出信号来。
这就是说理论上我们可以用持续时间为Ts的码元进行传输,而没有码间串扰;
根据这点,我们可以得到数字信号基带传输时,所占用的频带宽度是1/(2Ts) Hz,符号速率为1/T_s波特,其实也就是传输速率的1/2,用传输速率除以带宽,就得到频带利用率是2Band/Hz,1Hz的频带每秒最多只能传2个码元,这还是理想的极限值,这个带宽也称为奈奎斯特带宽。 此处证明完毕。(狗R的,注意低通滤波器的图是错的,它的截止频率应该是它标的一半,再次提醒)。
香农定理
噪声存在于所有的电子设备和通信信道中。
由于噪声是随机产生的,它的瞬时值有时会很大。
因此噪声会使接收端对码元的判决产生错误(1判决为0或0判决为1)。
噪声的影响是相对的,如果信号相对较强,那么噪声的影响就相对较小。因此,信噪比很重要,
香农定理给出了信道信息传送速率的上限(比特每秒)和信道信噪比及带宽的关系。香农定理可以解释现代各种无线制式由于带宽不同,所支持的单载波最大吞吐量的不同:
这里的B指信道带宽,单位Hz,同样也可以理解成B=\frac{1}{T} (单位symbol/s) 即单位时间内传输的符号个数,log_2(1+S/N) 表示给定信噪比条件下,每符号最大可传输的信息量(bit),即单位为(bit/symbol) ,为理解这一点,需要引入香农第二定理即编码定理:本科教材《通信原理》上:香农公式表明的是当信号与信道加性高斯白噪声的平均功率给定时,在具有一定频带宽度的信道上,理论上单位时间内可能传输的信息量的极限值、只要传输速率小于等于信道容量,则总可以找到一种信道编码方式,实现无差错传输。
参考其它:香农指出,任何一个通信信道都有确定的信道容量C,如果通信系统所要求的传输速率R小于C,则存在一种编码方法,当码长n充分大并应用最大似然译码(MLD,Maximum Likelihood Decoding)时,信息的错误概率可以达到任意小。
判断一种信道编码的好坏:码长足够长、码字足够随机化、采用最大似然译码。(北交慕课上有详细讲述)
附:香农限的概念:香农限是指单位时间单位带宽内传输1比特信息所需要的最小信噪比(Eb/N0)。即 \frac{E_b}{N_0}\ge \frac{2^{R_{b/B}}-1}{R_b/B}\left( B=1 \right) ,即通过给定单位带宽可传输的最大速率(bit/symbol),可计算获得无失真传输条件下的最小信噪比。常常用此参数来衡量不同信道编码的性能。
接下来从理论定义层面对香农定理进行分析:
不管是连续信道容量,还是离散信道,信道容量定义都是发送信号和接收信号的最大互信息,也就是:
\begin{array} { l } C = \max _ { p ( x ) } I ( X , Y ) 。 \\ \begin{array} { c } I ( X , Y ) = H ( Y ) - H ( Y \mid X ) = H ( Y ) - H ( X + Z \mid X ) = H ( Y ) - H ( Z \mid X ) \\ = H ( Y ) - \frac { 1 } { 2 } \log _ { 2 } ( 2 \pi e N ) \leq \frac { 1 } { 2 } \log _ { 2 } 2 \pi e ( P + N ) - \frac { 1 } { 2 } \log _ { 2 } ( 2 \pi e N ) \\ = \frac { 1 } { 2 } \log _ { 2 } \left( 1 + \frac { P } { N } \right) \end{array} \end{array}
这里对应的是实数信道。
若X,Y,Z都是复数,由于一个复数符号相当于两个实数符号,得到信道容量为
首先,实际现实的信号是实信号的,但是在数学建模过程中通常处理的是复数形式的信号。所以上式一般不用做实际应用中。
对于频带限制在B(Hz)的输入信号,按照理想情况下的抽样速率2B对信号和噪声进行抽样,将连续信号变为离散信号。此时连续信道的信道容量为:
- 互信息是信息论中用以评价两个随机变量之间的依赖程度的一个度量。
- 信息量:是对某个事件发生或者变量出现的概率的度量,一般一个事件发生的概率越低,则这个事件包含的信息量越大,这跟我们直观上的认知也是吻合的,越稀奇新闻包含的信息量越大,因为这种新闻出现的概率低。香农提出了一个定量衡量信息量的公式: log 1p=?log p
- 熵(entropy):是衡量一个系统的稳定程度。其实就是一个系统所有变量信息量的期望或者说均值。
单位:当log底数为2时,单位为比特; 但也用Sh、nat、Hart计量,取决于定义用到对数的底。
- 公式(离散变量): H(X)=∑_{x∈X}P(x)log 1P(x)=?∑_{x∈X}P(x)log P(x)=?ElogP(X)
- 当一个系统越不稳定,或者事件发生的不确定性越高,它的熵就越高。 以投硬币为例,正面的概率为?, 反面的概率则为?,那么这个系统的熵就是? 显然易得,当?时,?的取值最大,也就印证了 事件发生的不确定性越高,它的熵就越高。
- 对于连续变量?,?可以理解成它的概率密度函数,此时公式应该为: H(X)=∫P(x)?log P(x)dx
- 联合熵(joint entropy): 多个联合变量的熵,也就是将熵的定义推广到多变量的范围。 H\left( X,Y \right) =\sum{_{x\epsilon X}}\sum{_{y\epsilon Y}P\left( x,y \right)}\log \frac{1}{P\left( x,y \right)}=-E\log P\left( X,Y \right)
- 条件熵(conditional entropy):一个随机变量在给定的情况下,系统的熵。 \begin{aligned} H ( Y \mid X ) & = \sum _ { x \in X } P ( x ) H ( Y \mid X = x ) \\ & = \sum _ { x \in X } P ( x ) \left[ \sum _ { y \in Y } P ( y \mid x ) \log \frac { 1 } { P ( y \mid x ) } \right] \\ & = \sum _ { x \in X } \sum _ { y \in Y } P ( x ) P ( y \mid x ) \log \frac { 1 } { P ( y \mid x ) } \\ & = \sum _ { x \in X } \sum _ { y \in Y } P ( x , y ) \log \frac { 1 } { P ( y \mid x ) } \\ & = - E \log P ( Y \mid X ) \end{aligned} 不难看出,条件熵就是假设在给定一个变量下,该系统信息量的期望.
举一道例题:计算AWGN信道下BPSK的可达信息速率,
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。