数据代码分享|R语言回归分析:体脂数据、公交绿色出行与全球变暖2案例|附代码数据
原创数据代码分享|R语言回归分析:体脂数据、公交绿色出行与全球变暖2案例|附代码数据
原创
全文链接:http://tecdat.cn/?p=32520
原文出处:拓端数据部落公众号
通常在现实应用中,我们需要去理解一个变量是如何被一些其他变量所决定的。
最近我们被客户要求撰写关于回归分析的研究报告,包括一些图形和统计输出。
回答这样的问题,需要我们去建立一个模型。一个模型就是一个公式之中,一个因变量(dependent variable)(需要预测的值)会随着一个或多个数值型的自变量(independent variable)(预测变量)而改变的。我们能够构建的最简单的模型之一就是线性模型,我们可以假设因变量和自变量间是线性的关系。回归分方法可用于预测数值型数据以及量化预测结果与其预测变量之间关系的大小及强度。本文将介绍如何将回归方法应用到你自己的数据中,主要介绍学习内容:
用线性回归方法来拟合数据方程的基本统计原则和它们如何描述数据元素之间的关系。
如何使用R准备数据进行回归分析,定义一个线性方程并估计回归模型。
案例1:体脂数据回归分析
data=read.table("bodyfat.txt",header=F)给变量名赋值
{r}
colnames(data)=c("Density determined from underwater weighing","Percent body fat from Siri's (1956) equation","Age","Weight","数据相关图
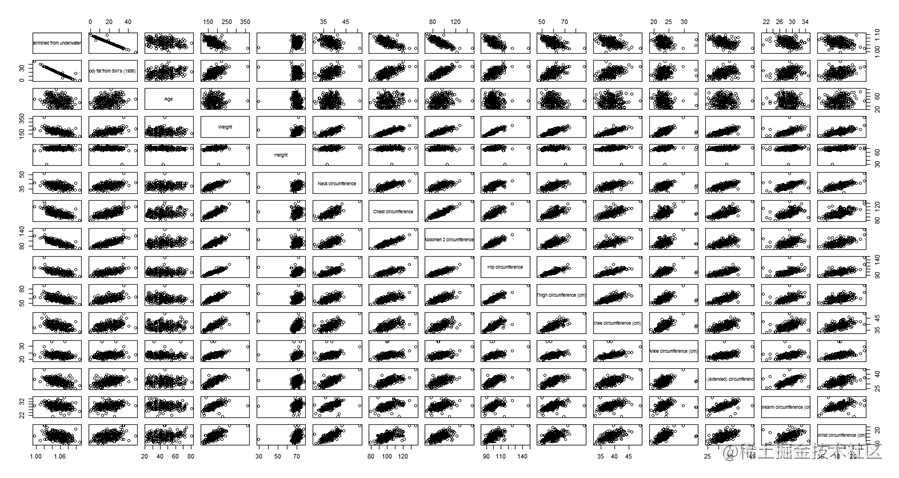
回归分析
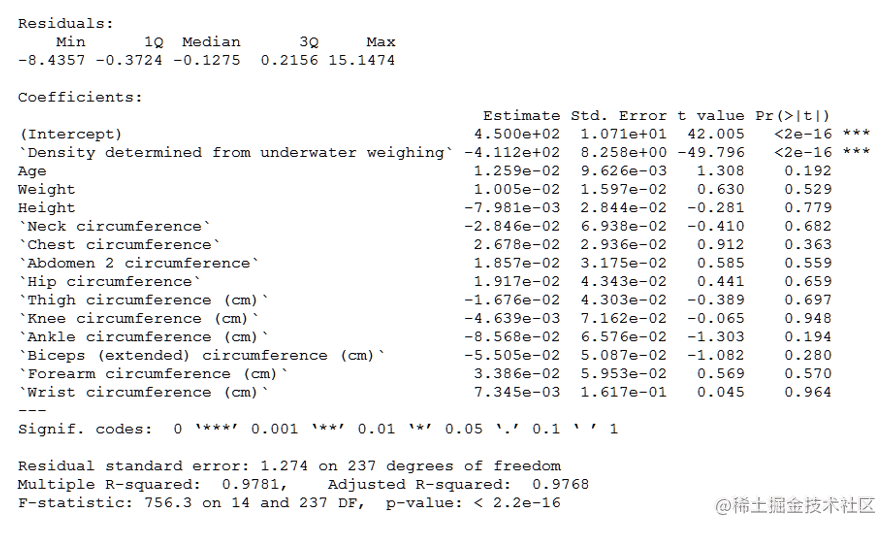
由于P<0.05,于是在α=0.05水平下,本例的回归系数有统计学意义,体重和体脂存在回归关系。
数据拟合图
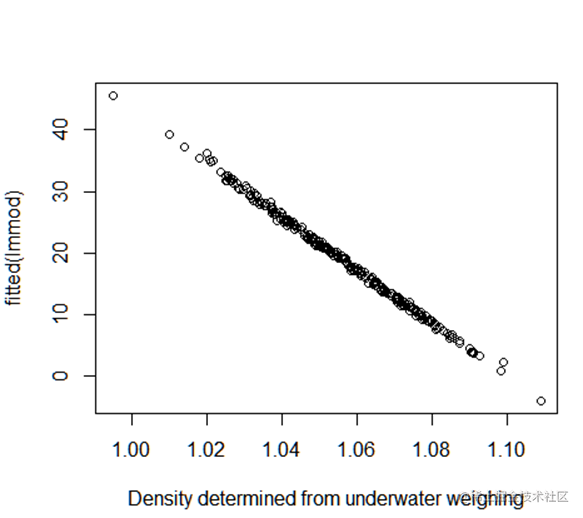
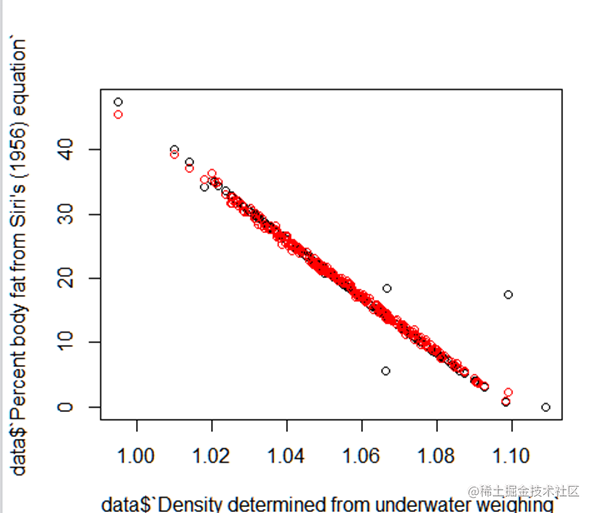
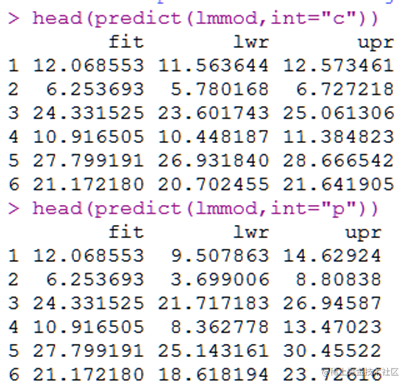
置信区间
残差分析
par(mfrow=c(2,2))
plot(lmmod)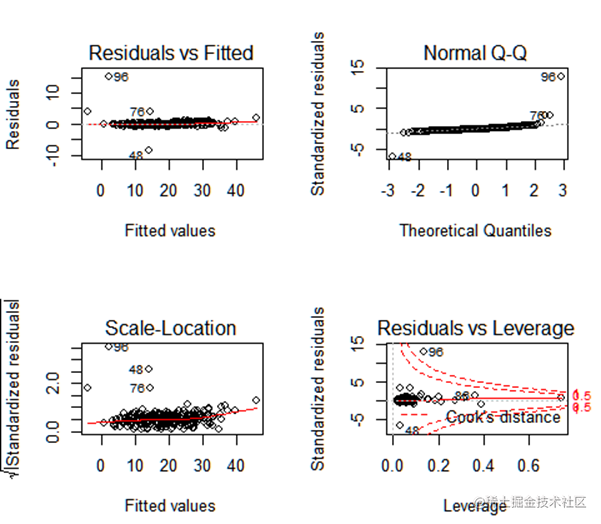
逐步回归
stepmod=step(lmmod,direction="both",trace=T);
由于P<0.05,于是在α=0.05水平下,本例的回归系数有统计学意义,体重、年龄、胸围和体脂存在回归关系。
案例2:公交绿色出行与全球变暖回归分析
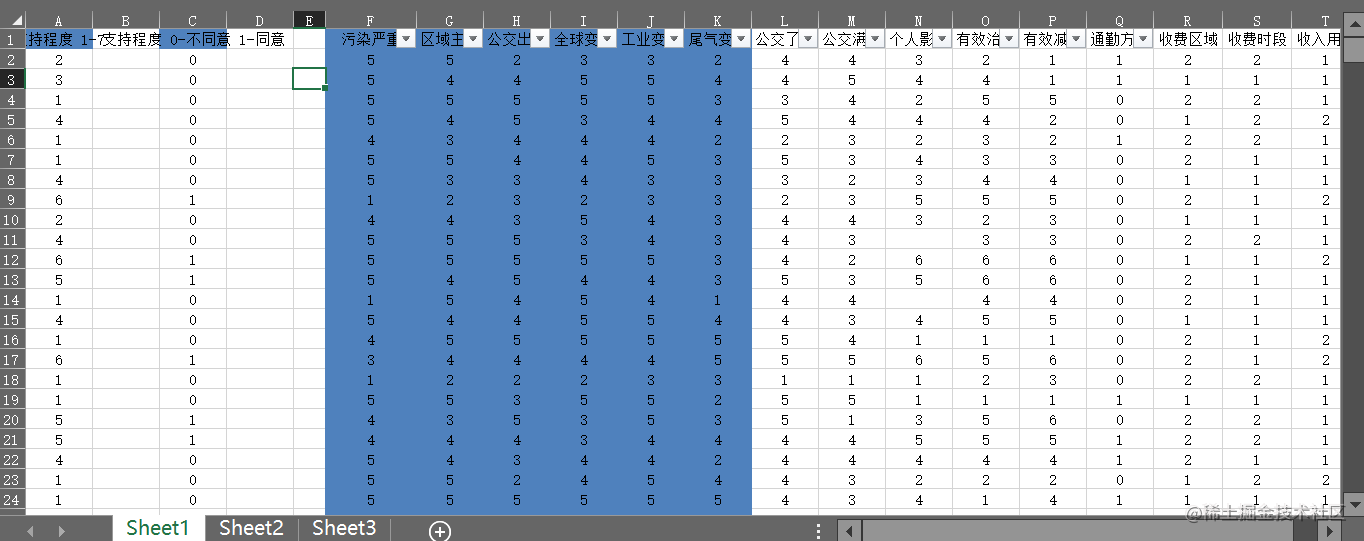
查看数据
head(data)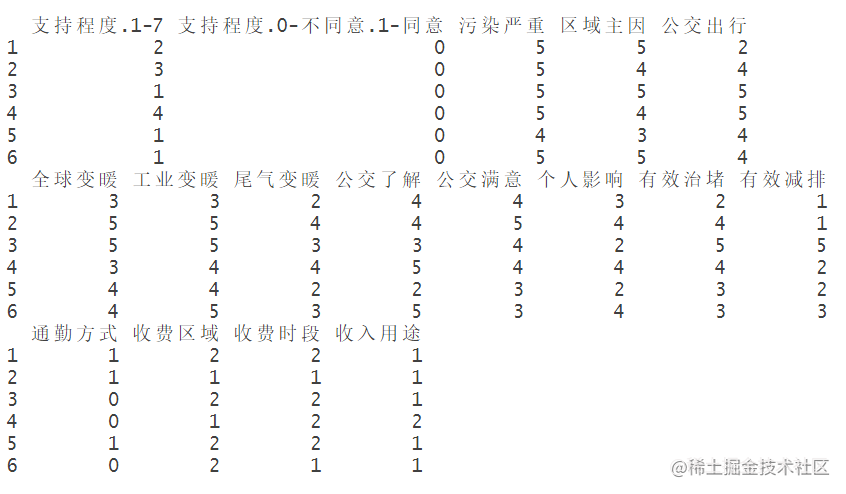
查看数据结构

查看数据概况

删除缺失数据
data[ data== "<NA>"]=NA
datanew=na.omit(data)相关分析
corrgram(datanew[,c("支持程度.1-7","污染严重"? ,"区域主因" ,"公交出行" , "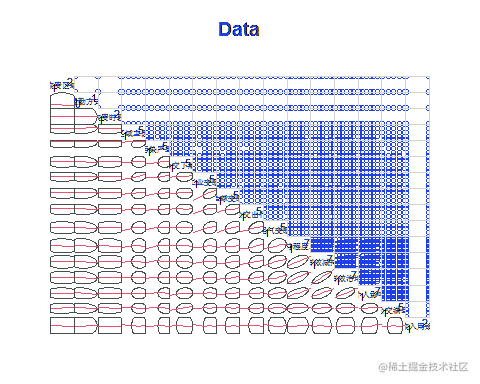
使用cor函数来查看不同变量之间的相关系数
##查看支持程度和不同变量之间的相关系数
cormat[1,]
## 支持程度.1-7???? 污染严重???? 区域主因???? 公交出行???? 全球变暖
##? 1.000000000? 0.057896120? 0.007793092? 0.195963899? 0.118643706
##???? 工业变暖???? 尾气变暖???? 公交了解???? 公交满意???? 个人影响
##? 0.038408531? 0.265162650 -0.028947130? 0.061299236? 0.561345590
##???? 有效治堵???? 有效减排???? 通勤方式???? 收费区域???? 收费时段
##? 0.647623352? 0.582528538 -0.067935998 -0.025646569 -0.086475704
##???? 收入用途
##? 0.064924787
cor.test(datanew$`支持程度.1-7`,datanew$公交出行)
##
##? Pearson's product-moment correlation
##
## data:? datanew$`支持程度.1-7` and datanew$公交出行
## t = 5.5525, df = 772, p-value = 3.875e-08
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##? 0.1272518 0.2628041
## sample estimates:
##?????? cor
## 0.1959639
cor.test(datanew$`支持程度.1-7`,datanew$全球变暖)
##
##? Pearson's product-moment correlation
##
## data:? datanew$`支持程度.1-7` and datanew$全球变暖
## t = 3.32, df = 772, p-value = 0.0009426
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##? 0.04858049 0.18754507
## sample estimates:
##?????? cor
## 0.1186437建立多元线性=======================因变量为支持程度.1-7
##获得训练集
?
train <- sample(1:nrow(datanew), nrow(datanew)*0.8)
datanew.train <- datanew[train, ]进行多元线性模型并进行分析 -----P值<0.1的和F-K列
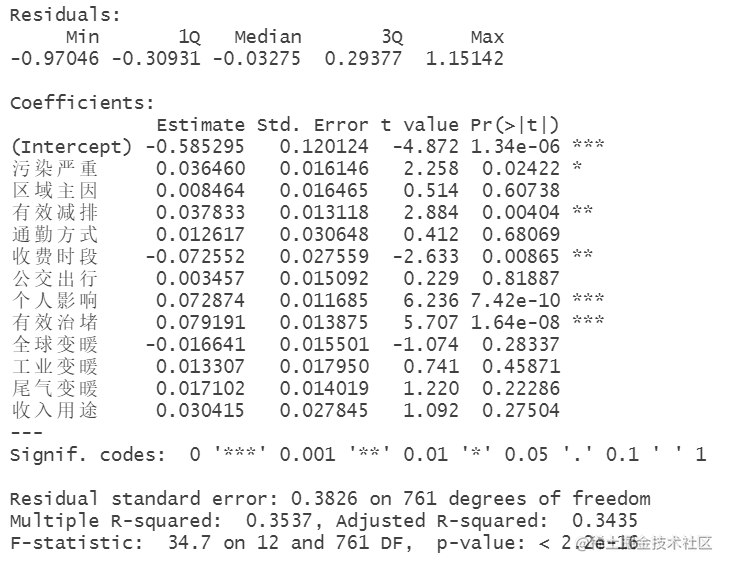
由于P<0.05,于是在α=0.05水平下,本例的回归系数有统计学意义,污染严重、有效减排、收费时段、个人影响和有效治堵和支持程度存在回归关系。
回归结果
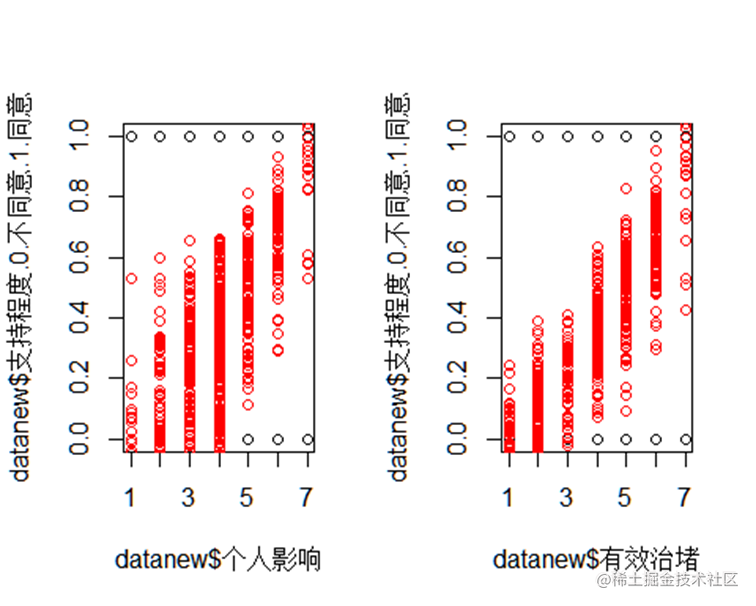
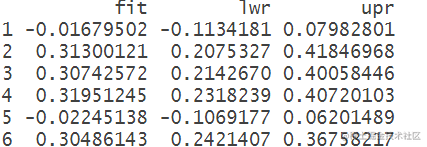
置信区间与预测区间:
置信区间是给定自变量值后,由回归方程得到的的预测值(实际上是的平均值)的置信区间;预测区间是实际值的置信区间,在这里称为预测区间。
残差分析:
残差分析可以对回归模型的假设条件即随机误差项是否独立同分布进行检验,同时还可以找出离群点。命令语句为plot(lm.1),显示结果如下
plot(lmmod)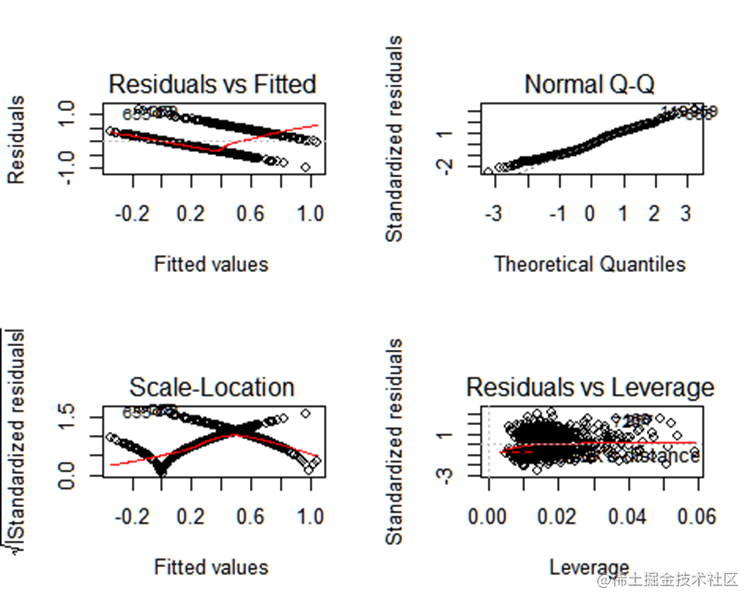
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。