密码学[3]:椭圆曲线
原创1 Short Weierstrass Curves
1.1 Affine Short Weierstrass form
Short Weierstrass 椭圆曲线:F 是特征 q > 3 的有限域,a, b ∈ F,且 4a^3 + 27b^2 \ne 0 ,所有点 (x, y) ∈ F x F 满足方程 y^2 = x^3 + ax + b 所组成的集合,还有额外的一个点 O,称为无穷点:
比特币的 secp256k1 曲线:用于生成 Bitcoin 的公钥,素数域 F_p :
p = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f需要 256 位二进制表示。secp256k1 曲线的参数为 a, b ∈ F_p, a = 0, b = 7 ,且 4 * 0^3 + 27 * 7^2 mod p = 1323 不等于 0:
阶为:
r = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141以太坊的 alt_bn128 曲线:定义于 EIP-19,素数域 F_p :
p = 0x30644e72e131a029b85045b68181585d97816a916871ca8d3c208c16d87cfd47需要 254 位二进制表示。alt_bn128 曲线的参数为 a, b ∈ F_p , a = 0, b = 73,且 4 * 0^3 + 27 * 3^2 mod p = 243 不等于 0:
阶为:
r = 0x30644e72e131a029b85045b68181585d2833e84879b9709143e1f593f0000001同构:F 是有限域,如果对于 (a, b) 和 (a^{'}, b^{'}) ,存在 c ∈ F^? ,使得 a^′ = a · c^4, b^′ = b · c^6 ,则椭圆曲线 E_{a, b}(F) 和 E_{a^′, b^′}(F) 是同构的。两者之间存在如下映射关系:
这种映射是 1:1 的,逆映射关系为 (x, y)\rightarrow (c^{-2}x, c^{-4}y)
点压缩:有的椭圆曲线上的点的坐标需要 256 位才能存下,我们也可以只存 x,y 根据式子算出来 \sqrt{x^3 + ax + b} ,因为该式子可能有两个值,所以还需要额外存一个符号位,0 表示选择接近 0 的值,1 表示选择 F 的阶的值。
1.2 Affine Group Law
弦和切线(chord-and-tangent)规则:地理定义,用符号 ⊕ 表示群运算
- 无穷处的点 O:定义为加法的中立元,对于所有的点 P ∈ E(F),有 P ⊕ O = P
- 弦规则:P 和 Q 是椭圆曲线上的两个点,且都不在无穷处,它们的和为:
- 穿过 P 和 Q 的直线 l 与椭圆曲线交于第 3 个点 R^′ ,R 为 R^′ 关于 x 轴的对称点,则 P ⊕ Q = R
- 如果直线 l 与椭圆曲线没有第 3 个点,则和为无穷点 O。
- 切线规则:P 事椭圆曲线上的点,且不在无穷处,点 P 和自身的和为:
- 直线 l 为椭圆曲线上在 P 处的切线,与椭圆曲线交于第 2 点 R^′ ,R 为 R^′ 关于 x 轴的对称点,则 P ⊕ P = R
- 如果 l 与椭圆曲线没有第 2 个点,则和为无穷点 O。
可见,椭圆曲线上的点和 ⊕ 构成交换群,无穷点 O 为中立元,每个元素的逆为关于 x 轴的对称点。
弦和切线(chord-and-tangent)规则:运算定义
- 中立元:无穷点 O
- 逆:无穷点 O 的逆是 O,非无穷点 (x, y) 的逆是 (x, -y)
- 群运算:对于 P, Q ∈ E(F)
- 中立元:如果 Q = O,那么 P ⊕ Q = P
- 逆:如果 P = (x, y),Q = (x, -y),则 P ⊕ Q = O
- 切线规则:如果 P = (x, y) 且 y != 0,则 P ⊕ P = (x', y′),其中,x' = (\frac{3x^2+a}{2y})^2 - 2x, y' =(\frac{3x^2+a}{2y})(x-x') - y
- 弦规则:如果 P=(x_1, y_1) ,Q=(x_2, y_2) ,且 x_1 \neq x_2 ,则 R = P ⊕ Q,其中 R=(x_3, y_3) ,x_3 = (\frac{y_2-y_1}{x_2-x_1})^2 - x_1 - x_2, y_3 = (\frac{y_2 - y_1}{x_2 - x_1})(x_1 - x_3) - y_1
(E(F), ⊕) 构成交换群,其中 F 为域,E(F) 为定义在域上的椭圆曲线。如果 Short Weierstrass 曲线上存在点 P = (x, 0),则称 P 是自逆的(self-inverse),因为 P ⊕ P = O,即逆就是自己。
标量乘法 Scalar multiplication:F 是有限域,E(F) 是椭圆曲线,阶为 n,生成器是 P,椭圆曲线标量乘法为(0P = O,mP = P + P + ... + P,是 P 与自身的 m 次相加):
对数顺序 Logarithmic Ordering:椭圆曲线的生成器是 g,阶为 n,元素具有对数顺序:
如果 P = lg,Q = mg,则 P ⊕ Q = l + mg,其中 l + m 是模 n 上的运算。
不过因为椭圆曲线是 DL-secure 的,所以对数顺序很难算出。
1.3 Projective Short Weierstrass form
无穷点相当于是射影集合中的原点,所以看下 Short Weierstrass 在射影几何的定义是有意义的。
F 是有限域,阶为 q,特征 > 3,a, b ∈ F 且 4a^3 + 27b^2 mod q \ne 0 ,FP^2 F 上的射影平面,则 F 上的射影 Short Weierstrass 曲线为所有点集 [X : Y : Z] ∈ FP^2 ,满足 Y^2 · Z = X^3 + a · X · Z^2 + b · Z^3 :
无穷点的射影坐标集为 [X : Y : 0],对于 (x_1 , y_1 , 0) ∈ [X : Y : 0] ,可以算出 0 = x_1^3 ,说明 X = 0,只有无穷点的射影坐标是类 [0, 1, 0] = {(0, y, 0) | y ∈ F}。点 [0 : 1 : 0] 是点在仿射中的无穷处 O 的射影形式。所以 Short Weierstrass 曲线的优点是不需要特殊的符号来表示仿射中的无穷点。
射影群法则 Projective Group law
在射影空间,所有的弦总是与曲线有 3 个交点,所有的切线总是与曲线有 2 个交点,所以不需要考虑额外的符号,数学上可以有所简化,代价是射影坐标或许没有那么直观。
可以证明,在射影空间中,椭圆曲线的点形成了一个关于弦和切线规则的交换群,射影点 0:1:0 是中立元,点 [X : Y : Z] 的加法逆是 [X : -Y : Z]。加法规则可用如下算法描述,使得加法和乘法的数量最小:
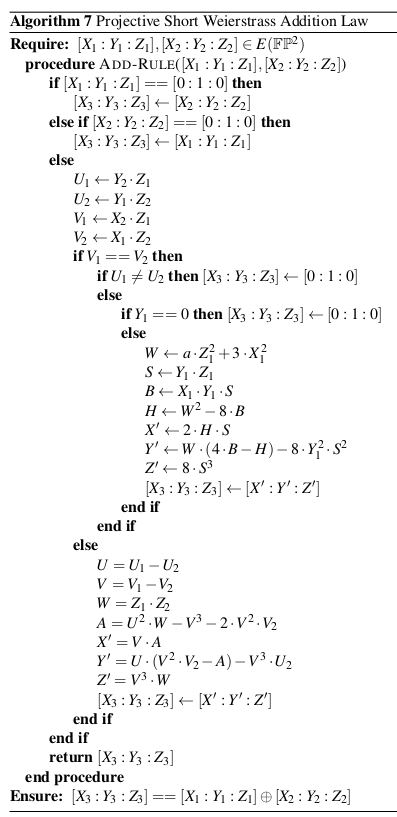
坐标转换 Coordinate Transformations
如果坐标 (x, y) 满足仿射 Short Weierstrass 方程 y^2 = x^3 + ax + b ,那么所有的同种坐标 (x_1, y_1, z_1) ∈ [x : y : 1] 满足射影 Short Weierstrass 方程 y^2_1 · z_1 = x_1^3 + ay_1 · z^2_1 + b · z^3_1
该映射是 1:1 的,所以存在逆映射:
I 和 I^{-1} 都遵守群结构,意味着 I(O) = [0 : 1 : 0] ,且 I((x_1, y_1) ⊕ (x_2 , y_2)) = I(x_1, y_1 ) ⊕ I(x_2, y_2 ) ,逆 I^{-1} 同样。
2 Montgomery Curves
仿射和射影 Short Weierstrass 形式上描述特征大于 3 的域上的椭圆曲线的最常见形式。但在某些情况下,为了获得更快的群算法或标量乘法,需要考虑更为特殊的椭圆曲线表示形式。
Montgomery 曲线可以在常数时间内计算椭圆曲线标量乘法。
Montgomery 曲线是所有可写成 Montgomery 形式椭圆曲线的子集。
F 为素数域名,阶为 p > 3,A, B ∈ F 是两个域元素,B != 0,A^2 != 4 mod p。F 上 的 Montgomery 曲线 M(F) 在其仿射表示中是满足 Montgomery 三次方程 B · y^2 = x^3 + A · x^2 + x 的所有点对集合和位于无穷处的点 O:
每个 Montgomery 仿射形式中的曲线都可以转为 Short Weierstrass 椭圆曲线形式:
但并不是每个素数域 F 上的特征 p > 3 的 Short Weierstrass 形式的椭圆曲线 E(F) = y^2 = x^3 + ax + b 都可以写成 Montgomery 形式。Short Weierstrass 曲线转成 Montgomery 曲线时,需满足如下条件:
- E(F) 上的点应被 4 整除
- 多项式 z^3 + az + b ∈ F[z] 至少有一个根 z_0 ∈ F
- 3z^2_0 + a 是 F^* 中的二次剩余
当这些条件都满足时,对于 $s = (\sqrt{3z^2_0 + a})^{?1}$,Montgomery 曲线定义如下:
Affine Montgomery coordinate transformation
如果 M_{A, B} 是 Montgomery 曲线,E_{a, b} 是 Short Weierstrass,其中 a = \frac{3-A^2}{3B},\space b=\frac{2A^2-9A}{27B^3} ,如下函数会将 Montgomery 上的点映射到 Short Weierstrass 上:
无穷点的映射也适用于上述式子。这种映射是 1:1,所以存在逆映射:
其中,z_0 是多项式 z^3 + az + b ∈ F[z] 的根,s = (\sqrt{3z^2_0 + a})^{?1} 。无穷点的映射也适用于上述式子。
Montgomery group law
Montgomery 曲线是 Short Weierstras 曲线的特殊形式,所以它的群运算也满足 chord-and-tangent 规则
- 中立元:无穷点 O 是中立元
- 逆元:O 的逆是 O。对于任何其它曲线上的点 (x, y) ,逆是 (x, -y)
- 群运算:对于任何两个曲线上的点 P, Q
- 中立元:如果 Q = O,那么和是 P ⊕ Q = P
- 逆元:如果 P = (x, y),Q = (x, -y),那么 P ⊕ Q = O
- 切线规则:如果 P = (x, y),y != 0,那么 P ⊕ P = (x′, y ′) 定义如下:
- 弦规则:如果 P = (x_1, y_1) ,Q = (x_2, y_2) ,x_1 \ne x_2 ,则 R = P ⊕ Q ,R = (x_3 , y_3 ) 定义如下:x' = (\frac{y_2 - y_1}{x_2 - x_1})^2 · B - (x_1 + x_2) - A, \space y' = \frac{y_2 - y_1}{x_2 - x_1}(x_1 - x') - y_1
3 Twisted Edwards Curves
Short Weierstrass 和 Montgomery 曲线的群运算都比较复杂。SNARK-friendly Twisted Edwards Curves 拥有易于实现的群运算,且不需要针对无穷点产生额外的运算分支。
F 为有限域,特征 > 3,a 和 d 是两个非 0 的域元素,Twisted Edwards 椭圆曲线点方式形式上所有来自 F x F 的满足 Twisted Edwards 方程 a · x^2 + y^2 = 1 + d · x^2 y^2 的点 (x, y) 集合:
当 a 是二次剩余,且 d 是二次非剩余时,Twisted Edwards 曲线是 SNARK-友好 Twisted Edwards 曲线
Twisted Edwards 曲线不需要额外的符号表示无穷点 (0, 1)。
Twisted Edwards 曲线等价于 Montgomery 曲线。
给定 Twisted Edwards 曲线后,Montgomery 曲线为:
给定 Montgomery 曲线 By^2 = x ^3 + Ax^2 + x ,B \ne 0, A^2 \ne 4 ,Twisted Edwards 曲线为:
Twisted Edwards group law
(x_1, y_1) 和 (x_2, y_2) 是 Edwards 曲线 E(F) 上的两个点,和为:
(x_1, y_1) 的逆元是 (-x_1, y_1)
点和其逆元相加是无穷点 (0, 1)
4 Elliptic Curve Pairings
Embedding Degrees
F 是有限域,阶为 q,E(F) 是 F 上的椭圆曲线,r 是 E(F) 的阶 n 的素因子,E(F) 的 embedding degree 是满足如下式子的最小的整数 k:
根据费马小定理,总是存在 embedding degree k(r),因为 k = r - 1 总是 q^k ≡ 1 (mod r ) 的解,即 q^{r-1} - 1 除以 r 后的余数是 0。
Elliptic Curves over extension fields
E(F) = \left\{(x, y) ∈ F × F | y^2 = x^3 + a · x + b \right\} 是仿射 Short Weierstrass 曲线,假如 F‘ 是 F 的扩展域,则 E(F') 为:
定义参数未发生改变。由于 F ? F′,所以 E(F) 是 E(F') 的子集。
Full torsion groups
F 是有限域,E(F) 是椭圆曲线,阶为 n,r 是 n 的因子。E(F) 上的 r-torsion 群是如下点集:
F_p 是素数域,E(F_p) 是椭圆曲线,只要 m 小于 E(F_p) 的 embedding degree k(r),那么 r-torsion 群 E(F_{p^m})[r] 就等于 E(F_p)[r] 。
回忆 F_{p^m} :其中的每个元素都可表示为字符串 <x_0,..., x_m> ,该字符串包含 m 个元素,每个元素都取自素数域 F_p 。
对于 p^{k(r)} ,r-torsion 群 E(F_{p^{k(r)}})[r] 包含了 E(F_p)[r] 的话,就称之为 full r-torsion 群:
对于任意 m > k(r),E(F_{p^m})[r] 都等于 E[r] ,所以 E[r] 就是最大的 r-torsion 群。full r-torsion 全包含 r^2 个元素和 r + 1 个循环子群。如下式子描述了所属关系:
对于 secp256k1,r-torsion 群是存不下的,因为每个元素都需要 k(r) · 256 bits 的空间。
Pairing groups
F 是有限域,特征为 p,E(F) 是椭圆曲线,其上的 Frobenius endomorphism(自同态) 定义如下:
π 将曲线点映射到曲线点。F 是素数域时,根据费马小定理有 (x^p, y^p) = (x, y) ,意味着 Frobenius 映射在素数域扩展的椭圆曲线上会更有趣些。
有了 Frobenius 映射,就可以刻画 full r-torsion 群 Er 的两个重要子群。第一个子群的元素来自 full r-torsion群,写作 G_1 ,假设给定素因子 r,G_1 定义如下:
G_1 就是素数域上未扩展的椭圆曲线的 r-torsion 群 E(F_p)[r] 。另一个子群是 full r-torsion 群,写作 G_2 :
如果 E(F) 是椭圆曲线,r 是曲线的阶的最大素因子,则 G_1[r] 和 G_2[r] 是配对群(pairing groups)简写为 G_1 和 G_2 。
The Weil pairing
E(F_p) 是椭圆曲线,embedding degree 为 k,r 是阶的素因子,Weil pairing 是如下的双线性,非退化映射:
Weil pairing 定义中的扩展域元素 f_{r,P}(Q), f_{r,Q}(P) ∈ F_{p^k} 可根据 Miller 算法算出:

如果存在群阶的素因子,使得 Weil pairing 相对于该质因子是可有效计算的,则称椭圆曲线 E(F_p) 是配对友好(pairing-friendly)。现实世界中,配对友好的椭圆曲线的 embedding degree 通常是小的数字,如 2,4,6 或 12,r 是曲线阶的最大素因子。
因为 secp256k1 不可能算出 G_2 ,更不可能算出扩展域 F_{p^k} ,所以 secp256k1 不是配对友好的。
5 Hashing to Curves
椭圆曲线密码学通常要求能够将数据哈希到椭圆曲线。如果椭圆曲线的阶不是素数,那么哈希到素数阶子群就很重要。在配对友好曲线中,哈希到配对群 G_1 或 G_2 也很必要。
一种方式是从基本域中选取 x 坐标,额外添加一位用来标识选取两个 y 坐标中的哪个。这种方式比较容易实现,但并不是所有的 x 坐标都能生成椭圆曲线上的点。其实在素数域上,只有一半的元素是二次剩余,所以这种方式有一半的概率会失败。
另一种方式是 try-and-increment 方法。如果哈希到域后不是合法的曲线点,那么增加计数器值,重复哈希,直到找到一个合法的曲线点:

如果曲线不是素数阶,那么生成的曲线点可能不位于大素数阶子群上。为了映射到大素数阶子群上,需要应用 cofactor clearing。
参考
The MoonMath Manual 第 5 章
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。
