0 - 1背包问题

什么是0 - 1背包

首先看一波百度词条对于 “0 - 1背包问题” 的阐述：

01背包是在M件物品取出若干件放在空间为W的背包里，每件物品的体积为W1，W2至Wn，与之相对应的价值为P1,P2至Pn。01背包是背包问题中最简单的问题。01背包的约束条件是给定几种物品，每种物品有且只有一个，并且有权值和体积两个属性。在01背包问题中，因为每种物品只有一个，对于每个物品只需要考虑选与不选两种情况。如果不选择将其放入背包中，则不需要处理。如果选择将其放入背包中，由于不清楚之前放入的物品占据了多大的空间，需要枚举将这个物品放入背包后可能占据背包空间的所有情况。

是不是比较懵，那我们再对比地看一下 “背包问题” 帮助理解：

背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。相似问题经常出现在商业、组合数学，计算复杂性理论、密码学和应用数学等领域中。也可以将背包问题描述为决定性问题，即在总重量不超过W的前提下，总价值是否能达到V？它是在1978年由Merkle和Hellman提出的。

简单来说背包问题就是能将物品分割成一部分装入背包（实现部分装入使得价值最大化），而 0 - 1背包呢，顾名思义，只有 0 （不装） 和 1（装入） 两种选择（这里我们讨论普通背包：一件物品只能被装入一次）；

解决实际问题

假设你现在有一个容量为8（指最多可装质量）的背包，摆在你面前的是一些有着不同质量且价值不等的物品，具体信息用数组表示为weight = [ 2, 3, 4, 5] , 对应价值 value = [ 6, 7, 6, 7]，现在的问题是如何装包使得价值最大化？

贪心思路

这里我们是不能使用贪心算法的，若我们使用一种贪心策略：始终选择当前物品中 rate = (value / weight) 最大的，也就是单位价值最大的物品。那么每种物品的单位价值为 unitVal = [ 3, 2.3, 1.5, 1.4]；

据此我们首先选择 0号物品（编号从0开始），剩余容量为 8 - 2 = 6；紧接着选择 1号物品，背包剩余容量为 6 - 3 = 3;由于不可重复装包，剩下的两件物品我们无法再装入，得到最终结果 6 + 7 = 13，很显然这是不对的，因为我们可以选择1号与3号物品得到最大价值7 + 7 = 14；

动态规划求解

1. 确定dp数组以及下标的含义

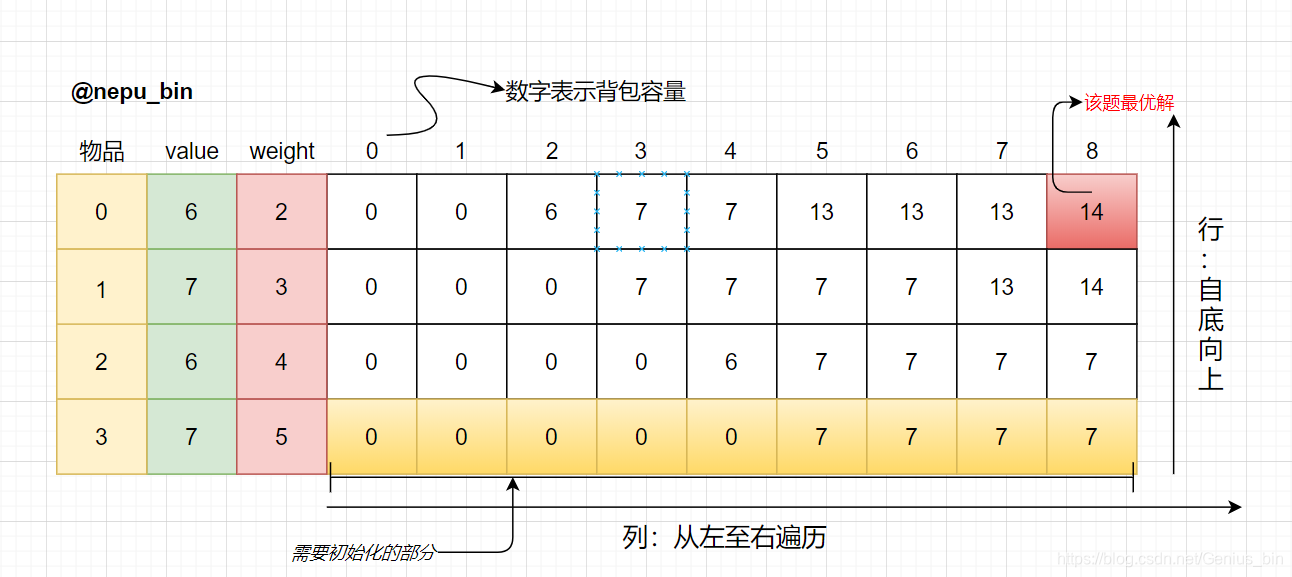
这里涉及到背包容量c以及物品重量两个维度，我们使用二维数组来记录每一次选取得到的最大价值，二维数组的每一行表示一种物品，共计 weight.size() 行，数组的每一列表示背包的容量，共计 c （背包容量）+ 1列，dp[i][j]表示在编号从 i 到 最后一号物品所构成的物品集合中且背包容量为j时取得的最优解.即从 [i : 最后一号物品] 中任意取，放进容量为 j 的背包里，价值总和最大是多少。 如dp[2][5] 表示 当背包容量为 5 时从 2 ~ 3 号物品选择出的最大价值；同理， dp[1][8] 表示 当背包容量为 8 时从 1 ~ 3 号物品选择出的最大价值。

2. 确定递推公式
若当前背包容量不足以放下当前物品时（c < weight[i]）我们只能等于背包容量等于 c 且为装入当前物品时的最优解；而当背包容量可以放下当前物品时 （c >= weight[i]），我们有两种选择：装入当前物品 or 不装入；将当前物品装入后，背包还剩余的容量我们也能创造一定价值，这就要依赖dp数组中之前的解情况了，而选择不装入，就与上一种情况一样继承了之前的最优解，而我们需要两者的最大值。
因此dp公式为：

3、dp数组如何初始化&&确定遍历顺序
根据第一点中叙述的dp数组的含义，当背包容量为0的时候不能装入任何物品，初始化 dp[i][0] = 0;

//注：row 为dp的行数，col 为dp的列数
for (int j = weight[row - 1]; j < col; ++j) {//当背包容量刚好放下最后一号物品时
		//初始化dp数组 
		dp[rindex][j] = value[rindex];
	}

遍历顺序：从dp数组最后一行从左往右自底向上(这里无特殊要求，行方向也可以从上往下遍历)
根据递推公式 dp[i][j] = max(dp[i + 1][j] , dp[i + 1][j - weight[i]] + value[i]) 以及遍历顺序，我们遍历第 i 个物品时可能需要用到 “i + 1” 个物品的解情况，因此我们遍历之前需要对dp数组最后一行进行初始化；
具体解释见代码；

dp数组详情（读者可自己根据递推公式推导）：

#include <iostream>
#include <vector>
using namespace std;
//回溯背包装包过程，将状态记录到x数组中
void traceBack(vector<vector<int>>& dp, vector<int>& weight, vector<int>& x, int c) {
	int len = x.size();
	for (int i = 0; i < len - 1; i++) {
		if (dp[i][c] == dp[i + 1][c])
			x[i] = 0;
		else {
			x[i] = 1;
			c -= weight[i];
		}
	}
	x[len - 1] = (dp[len - 1][c] ? 1 : 0);
}

int ZeroOneKnapsack(vector<int>& weight, vector<int>& value, int c, vector<vector<int>>& dp) {
	//row行 c + 1列数组
	int row = dp.size(), col = dp[0].size();
	int rindex = row - 1;
	for (int j = weight[row - 1]; j < col; ++j) {//当背包容量刚好放下最后一号物品时
		//初始化dp数组
		dp[rindex][j] = value[rindex];
	}
	rindex--;
	//rindex即 行下标 ，cindex为列下标
	for (; rindex >= 0; rindex--) {
		for (int cindex = 0; cindex < col; cindex++) {
			if (cindex < weight[rindex]) {
				//当前容量不足以装下当前物品，价值来源于上一行（此处没装）
				dp[rindex][cindex] = dp[rindex + 1][cindex];
			}
			else {
				//两种情况：1、装入当前物品，当前物品的价值加上剩余容量能创造的价值
				//2、不装入当前物品，价值等于dp数组上一行的数值
				dp[rindex][cindex] = max(dp[rindex + 1][cindex], dp[rindex + 1][cindex - weight[rindex]] + value[rindex]);
			}
		}
	}
	return dp[0][col - 1];
}

int main() {
	vector<int> weight{ 2,3,4,5 };//各物品质量
	vector<int> value{ 6,7,6,7 };//对应物品的价值
	int c = 8;//背包容量
	vector<vector<int>> dp(weight.size(), vector<int>(c + 1));//创建二维dp数组
	cout << "背包可以装入物品的最大价值为" << ZeroOneKnapsack(weight, value, c, dp) << endl;
	vector<int> x(weight.size(), 0);//记录物品的装包情况 
	traceBack(dp,weight,x,c);
	for (int i = 0; i < x.size(); i++) {
		if (x[i])
			cout << i << "号物品被放入背包, 价值为" << value[i] << endl;
	}
	return 0;
}

运行效果

空间优化

这里使用的二维数组实质上可以用一个一维数组代替，根据递推公式

当前背包的最大值取决于上一次遍历得到的最优解， 使用一维动态数组时需要注意：不能再从左至右遍历：
假设当前遍历的物品编号为i，weight[i] = 1，价值value[i] = 15, 且dp[0] = 0;
如从左至右遍历：（dp[i] 表示 背包容量为 i 时取得的最大值）

• dp[1] = max(dp[1 - 1], dp[1 - weight[i] ] + value[i]) = dp[0] + 15 = 15; 1 >= weight[i];
• dp[2] = max(dp[2 - 1], dp[2 - weight[i] ] + value[i]) = dp[1] + 15 = 30; 2>=weight[i]
  很显然这里对当前物品进行了重复装包，而在当前问题中这是不允许的，所以我们必须从右往左逆序遍历，可以根据递推公式尝试推导从右往左遍历时dp数组的取值情况（避免了重复取同一个物品）；

代码如下：

int ZeroOneKnapsack(vector<int>& weight, vector<int>& value, int c) {
	int nums = weight.size(), col = c + 1;
	vector<int> dp(c + 1, 0);//初始化一维数组dp长度为 c + 1且所有元素为0
	int curNo = nums - 1;//当前遍历的物品编号
	for (int i = nums - 1; i >= 0; i--) {//当前物品
		for (int j = c; j >= weight[i]; j--) {//背包当前容量
			dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
		}
	}
	cout << dp[c] << endl;
	return dp[c];
}

说明（小声bb）

科班大二在读，菜鸟一名，正修算法，博客主要用于记录自己对于一些经典题的理解和以及提升代码实现能力，均为课后根据思路（思路来源：上课老师讲解、课下查阅相关资料）原创完成，有表述不清或思路混乱的地方还请宽恕以及评论告知，一起学习一起进步，欢迎大家指正~~~